Una “estructura de datos” es una colección de valores, la relación que existe entre estos valores y las operaciones que podemos hacer sobre ellos; en pocas palabras se refiere a cómo los datos están organizados y cómo se pueden administrar. Una estructura de datos describe el formato en que los valores van a ser almacenados, cómo van a ser accedidos y modificados, pudiendo así existir una gran cantidad de estructuras de datos.
Lo que hace específica a una estructura de datos es el tipo de problema que resuelve. Algunas veces necesitaremos una estructura muy simple que sólo permita almacenar 10 números enteros consecutivamente sin importar que se repitan y que podamos acceder a estos números por medio de un índice, porque nuestro problema a resolver está basado en 10 números enteros solamente. O tal vez nos interese almacenar N cantidad de números enteros y que se puedan ordenar al momento de insertar uno nuevo, por lo que necesitaremos una estructura más flexible.
¿Por qué son útiles las estructuras de datos?
Las estructuras de datos son útiles porque siempre manipularemos datos, y si los datos están organizados, esta tarea será mucho más fácil.
Considera el siguiente problema:
¿De qué forma puedo saber si una palabra tiene exactamente las mismas letras que otra palabra? O dicho de otra forma, ¿cómo saber si una palabra es una permutación de otra palabra?.
Si queremos resolver este problema con papel y lápiz, basta con escribir las palabras y visualmente identificar si ambas palabras tienen las mismas letras, una forma rápida es contar mentalmente el número de cada tipo de letra en ambas palabras y si tienen el mismo número entonces si es una permutación.
Pero si quisiéramos resolverlo mediante programación tenemos que decirle a la computadora como saber que es una palabra y decirle cómo debe comparar las palabras de la misma forma en que lo resolvimos en papel y lápiz, ¿Se te ocurre alguna forma?.
Qué tal si pensamos en las palabras como una estructura de casillas de letras secuenciales (array ó arreglo) donde cada letra representa una casilla en esta estructura. A cada casilla le damos un índice con el cual podemos acceder a ella para saber qué letra tiene contenida, esto le indicará a la computadora cómo reconocer una palabra.
Ahora, para resolver el problema debemos saber cómo comparar las palabras y sus letras, lo primero que podemos evaluar es el length ó longitud de la palabra, o sea, cuántos caracteres tiene; si las palabras tienen diferente número de caracteres entonces no tiene sentido comparar más, ya sabemos que NO tendrán exactamente las mismas letras. Lo siguiente será contar las letras por tipo de letra. En el ejemplo anterior de las palabras “casa” y “saca” contamos las letras mentalmente, pero las escribimos en el papel con una estructura muy específica, cada letra que encontramos se asocia al número que contamos; entonces, ¿habrá alguna estructura de datos que me ayude a asociar las letras con el número que contamos?, la respuesta es sí.
Podemos pensar en esta asociación como una estructura de tipo key-value (llave-valor) llamada dictionary ó diccionario, donde la letra es la llave y su valor asociado es el número contado; además, en esta estructura no debemos repetir la llave porque de lo contrario tendremos letras repetidas y no podremos contar, es por eso que la estructura dictionary es distinta al array, ya que en el array si podemos repetir letras, pero en esta otra estructura no deberíamos permitirlo ya que eso sería lo que nos permita resolver el problema de contar.
De modo que para operar la estructura array tenemos que hacerlo recorriendo una a una todas las casillas para obtener las letras mediante su índice; la casilla 0 contiene a la letra “c”, la casilla 1 contiene la letra “a” y así sucesivamente. Para el caso de la estructura dictionary podemos decir que vamos a operar en ella a través de su key (llave); la llave “c” tiene asociado el valor 1, la llave “a” tiene asociado el valor 2, y así sucesivamente. Cada vez que encontremos una letra la pondremos en la estructura dictionary, si no existe se agrega y se asocia con el valor 1, sí ya existe entonces “contamos” y a su valor le sumamos +1.
Hasta este punto las estructuras de datos nos han ayudado a resolver este problema con el simple hecho de tener nuestros valores organizados y definiendo la forma en la que podemos operar sobre ellos; aún quedan varios pasos más para resolver el problema por completo pero eso pasa a ser objeto de otro tema en programación que son los algoritmos. Por ahora nos basta con identificar las estructuras de datos.
Tipos de estructuras de datos
Al hablar de estructuras de datos debemos pensar en primera instancia en cómo los datos se representan en la memoria, ¿se trata de estructuras contiguas o enlazadas?, al partir de esta pregunta podemos darnos la idea correcta sobre la base de nuestra estructura y cómo es que los datos se van a almacenar.
- Las estructuras contiguamente asignadas están compuestas de bloques de memoria únicos, e incluyen a los arrays, matrices, heaps, y hash tables.
- Las estructuras enlazadas están compuestas de distintos fragmentos de memoria unidos por pointers ó punteros, e incluyen a los lists, trees, y graphs.
- Los contenedores son estructuras que permiten almacenar y recuperar datos en un orden determinado sin importar su contenido, en esta se incluyen los stacks y queues.
Debo aclarar que esta es una clasificación muy específica basada en el libro “The Algorithm Design Manual de Steven S. Skiena”, después de leer distintas clasificaciones esta es la que se me hizo más sencilla y fácil de comprender.
En internet podrán encontrar una lista larga de estructuras de datos, sin embargo en este post sólo abarcaremos las mas conocidas y esenciales para entender este concepto, ¡Comenzamos!.
Array
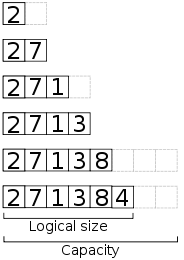
Esta estructura es “la” fundamental de las estructuras contiguamente asignadas. Arrays ó arreglos son estructuras de datos de tamaño fijo de modo que cada elemento puede ser eficientemente ubicado por su index (índice) ó dirección. Exactamente como lo vimos en el ejemplo anterior un array tiene una tamaño fijo y una dirección (index) con la cual podemos localizar de forma rápida un elemento en el arreglo, de modo que podemos apuntar a un elemento en el array de la siguiente forma: array[index], donde array es el nombre de nuestra estructura, seguida de dos “corchetes” que abren y cierran, donde especificamos el index que deseamos apuntar.
Los arrays muestran algunas ventajas con respecto a otras estructuras, como por ejemplo:
- Al tener un espacio contiguo en memoria cada index de cada elemento del array apunta directamente a una dirección de memoria, de esta forma podemos acceder arbitrariamente a los datos de forma instantánea puesto que sabemos la dirección de memoria exacta. Esto deriva en un acceso de tiempo constante dado por los index.
- Los arrays son puramente datos lo que significa que no es necesario desperdiciar espacio en memoria almacenando información extra que ayude a la localización de sus elementos como es el caso de las estructuras enlazadas, los arrays tienen eficiencia de espacio.
- Localidad de memoria, es común que en la programación los datos de una estructura sean iterados (o recorridos) y los arrays son buenos para esto ya que exhiben excelente localización de memoria, permitiéndonos aprovechar la alta velocidad de la caché en computadoras modernas.
La gran desventaja de los arrays es que no podemos ajustar su tamaño a la mitad de la ejecución de un programa, pero ¿y qué tal si creamos uno nuevo con la nueva dimensión deseada?; esto sería bueno si supiéramos el tamaño que deseamos todo el tiempo, pero si no lo sabemos sólo tenemos 2 opciones: crear una array lo suficientemente grande para almacenar nuestros datos, pero esto deriva en un desperdicio de memoria totalmente innecesario, ó podemos crear un nuevo array, doblar el tamaño de éste cada vez que se necesite crecer y copiar los datos del array anterior al nuevo array, hacer esto tiene el mismo nivel de complejidad que si tuviéramos un array único suficientemente grande, pero con la ventaja de que sólo va a crecer cuándo sea necesario, evitando así desperdiciar memoria. Es pues que de esta forma podemos alargar un array en tiempo de ejecución, a este concepto se le conoce como dynamic arrays ó arreglos dinámicos.
Los arrays son la base de muchos otros tipos de estructuras de datos como acabamos de ver con los arreglos dinámicos.
Otra estructura muy común que nos ayuda a representar datos reales son las llamadas matrices o tablas que no son mas que arrays de múltiples dimensiones. Pensemos, si un arreglo es una colección consecutiva de valores, se puede decir que son de tipo lineal en una dimensión plana ó uni-dimensionales, si quisiéramos formar una matriz o tabla (matrix o table) podríamos crear un array bi-dimensional, lo que quiere decir que tendremos que localizar a un elemento por su index [i , j], o bien su ubicación lineal a la derecha y hacia abajo como en un plano cartesiano con dimensiones xy asemejando a una tabla, o podríamos crear un array tri-dimensional, agregando una dimensión más de “fondo”, que haría que localizáramos a un elemento en su index [i, j, k], en plano cartesiano como xyz. Además existe una tercer clasificación conocida como jagged arrays o matrices dentadas como se ve en la siguiente imagen, donde vemos un arreglo de tipo bi-dimensional pero con la diferencia de que una de sus dimensiones no es rectangular sino que puede tener distintos tamaños formando así una matriz dentada.
Puedo decir que este es un resumen sobre los arrays, uno que sin duda nos ayudará a identificar de forma más rápida el tipo de “array” que necesitamos usar.
Estructuras enlazadas (linked structures)
La magia de las estructuras enlazadas es dada por los pointers o punteros, que como su nombre lo indica apuntan a una dirección de memoria donde se encuentra ubicado un valor. Los pointers son los encargados de mantener los “enlaces” entre valores de modo que es posible tener una secuencia de valores todos enlazados por pointers. Si ponemos atención a la definición de los pointers podemos deducir que los valores no necesariamente tienen que estar localizados en memoria uno después del otro como en le caso de los arrays que son contiguamente asignados, por lo que podemos tener los valores ubicados en distintas localidades de la memoria y aún así representar un colección de valores consecutivos.
Como se observa en la imagen, tenemos una secuencia de valores enlazados por pointers llamados nodos, que están representados por un cuadro vacío y una flecha. El cuadro vacío representa el valor con la dirección de memoria a donde está apuntando el valor que contiene, de modo que: el valor 12 está enlazado por medio de un pointer que guarda la ubicación del siguiente valor en la secuencia que es el 19 y este a su vez guarda la ubicación al valor 37. Cuando hablemos de estructuras enlazadas debemos siempre pensar en que además de almacenar el valor que deseamos, debemos tener un espacio extra donde debemos almacenar la dirección de memoria del siguiente valor.
Después de una breve introducción a los pointers podemos pasar a la estructura mas común de las estructuras enlazadas que son las linked lists o listas enlazadas.
Linked lists
Comencemos por definir una “lista”. Una lista es aquella estructura que representa un número contable de valores ordenados donde un mismo valor puede repetirse y considerarse un valor distinto a otro ya existente. Las listas son consideradas secuencias de valores y cómo ya veíamos en la explicación anterior sobre pointers estos se pueden aplicar para implementar una lista de tal forma que las características principales de una lista serían:
- Cada nodo en nuestra lista contiene uno o más campos que contienen el valor que deseamos almacenar.
- Cada nodo contiene al menos un campo pointer apuntando a otro nodo, lo que significa que podemos tener 2 pointers, uno que apunta a un nodo consecuente y otro que apunta a un nodo previo formando así una lista doblemente enlazada (double linked list).
- Es necesario tener un pointer que apunte a la cabeza de la estructura para así saber por dónde comenzar.
¿Recuerdan cuando explicábamos el problema de la permutación de una palabra?, específicamente cuando hablábamos de representar una palabra en un array donde cada letra era una casilla, bien, aquí tenemos una lista de palabras lo cual puede claramente significar que es una lista de arrays. La mayoría de los lenguajes de programación representan a las “cadenas” (palabras, secuencia de caracteres, etc) como arrays de caracteres, es por eso que con otra estructura como las lists podemos tener secuencias de palabras pudiendo representar un párrafo de un libro o de un post de medium que habla sobre estructuras de datos :p
Ahora debo mencionar que las 3 operaciones básicas soportadas por una linked list son: búsqueda, inserción y eliminación de nodos. Suena obvio ¿no creen?, para explicar esto haré una comparación sobre ambos tipos de estructuras y quizá así quede más claro.
Array vs Linked list
- Una diferencia grande entre los arrays vs linked lists es que insertar o eliminar de una linked list es más fácil ya que no tiene tamaño fijo y lo único que debemos hacer para insertar o eliminar un valor es simplemente apuntar al nuevo nodo creado, ó apuntar al siguiente nodo de la lista si un nodo fue eliminado. En un array no existe esta flexibilidad.
- Si tenemos una gran cantidad de valores siempre será más fácil mover pointers de una valor a otro que mover los valores en sí.
- En un array podemos provocar un desbordamiento de memoria (memory overflow) si queremos insertar un valor extra y ya hemos excedido el tamaño del array, lo cual no sucedería en una linked list.
- Por otro lado en una linked list necesitamos más espacio en memoria para almacenar los pointers.
- Los arrays tienen un mejor manejo del acceso aleatorio a los valores y son mucho mejores en la ubicación de los datos en memoria y aprovechamiento de la caché.
¿Cuál es mejor? Ninguna es mejor que la otra, todo dependerá de lo que necesitemos resolver. Imaginemos que estamos creando una estructura para almacenar los usuarios de nuestra aplicación, esta estructura debe guardar el username y su password, ya dijimos que las linked list son rápidas para insertar y eliminar, entonces ¿usaríamos una linked list?, si podríamos. Ahora si usáramos la linked list y quisiéramos obtener un username porque queremos saber su password para el log-in de nuestra aplicación ¿sería mejor usar un array?, el acceso en los arrays es más rápido ya que sabiendo la ubicación obtendremos el dato directamente, cosa que en la linked list no podríamos.
Entonces, ¿cómo resolvemos este problema si queremos insertar y eliminar de forma eficiente, y también queremos acceder a los datos de forma eficiente?, podríamos combinar ambas estructuras, sí, hacer un array de linked list.
De esta forma podríamos asignar a cada casilla del array una linked list por cada letra del abecedario, si deseamos agregar un username “Marcela” iríamos directamente a la casilla de la letra M e insertaríamos un nuevo nodo con el username y su password en la linked list. Y si queremos obtener el username podemos de nuevo ir a la casilla de la M y buscar en el linked list. De esta forma evitaríamos buscar en todos los usernames hasta encontrar el que queremos, y obtener y agregar nuevos datos se volvería mas fácil y rápido.
Contenedores
Las estructuras de tipo contenedor se caracterizan principalmente por la forma particular de recuperación ordenada de datos que soportan, y en los dos tipos principales de contenedores (stack y queue) el orden de recuperación depende del orden de inserción.
Stack
Un stack o pila, soporta la recuperación ordenada de datos last-in, first-out (LIFO) o bien: el último dato en entrar, el primer dato en salir. De la misma forma en que se hace en una pila de platos limpios, si necesitamos un plato limpio vamos a la pila y tomamos el primero de la pila, que en realidad fue el último plato que agregamos a ella. Las pilas son estructuras que encontramos de muchas formas en el mundo real, siempre que podamos apilar algún objeto como libros, cazuelas, películas o la forma en la que metemos latas de refresco en el refrigerador 🙂
Tomando en cuenta lo anterior podemos pensar que si usamos un stack es porque probablemente el orden de la recuperación de datos no nos importa tanto, simplemente queremos apilarlos y des-apilarlos, por lo que las operaciones fundamentales en un stack son push y pop para poner y obtener datos de la pila.
Con push() insertamos un elemento en el tope de la pila, y con pop() retornamos y removemos el elemento en el tope de la pila, como se ve en la imagen.
Queue
Una queue o cola, soporta la recuperación ordenada de datos first-in, first-out (FIFO) o bien: el primer dato en entrar, es el primer dato en salir. Justo como una cola en el banco cuando vamos a realizar alguna operación con nuestra cuenta bancaria, si todos los asistentes están ocupados se genera una cola donde el primero que llegó será el primero en ser atendido y el resto esperamos en la cola. Este tipo de estructuras se utiliza mucho en el control de tiempos de espera de servicios, tiempos de ejecución en un CPU, de conexión de red, o en el mundo real en una cola para las tortillas, para entrar en una avenida rápida, etc.
En este tipo de estructura el orden sí importa, pues siempre el primero de la cola debe ser el primero en ser atendido y el resto de forma ordenada esperan su turno. Las operaciones de esta estructura son: enqueue y dequeue para encolar y des-encolar (poner y obtener de la cola).
De modo que enqueue() inserta un elemento al final de la cola, y dequeue() retorna y remueve el primer elemento de la cola.
Conclusión
Las estructuras de datos existen para ayudarnos en la compleja tarea de resolver problemas en programación, no importa el lenguaje de programación que utilices, si vas a manejar datos de cualquier tipo siempre caerás en el uso de estructuras de datos. Dicho esto, podemos concluir que tener una base sólida de entendimiento sobre las características de una estructura de datos nos llevarán a hacer la mejor elección para resolver nuestro problema, y de esta forma alejarnos de hacer una mala elección que nos pueda costar mucho: mucha memoria, mucho tiempo de ejecución, mucho tiempo de desarrollo.
En una segunda parte, escribiré sobre los diccionarios, hash tables, árboles y grafos.