Curso 2 Estructura de datos — Dictionaries, Trees, Graphs 2020

En esta segunda parte de estructuras de datos explicaré de forma clara pero concisa los diccionarios, árboles y grafos. Continuaremos con la misma línea del post anterior abordando ejemplos, diferencias y características principales. Al fnalizar la lectura de este post podrás darte cuenta de la importancia de estas estructuras, además de darte una idea más clara de cómo y dónde se pueden usar.

Quizá descubras que ya las estás utilizando y lo comunes que son en el día a día, en las aplicaciones que usas o que desarrollas. ¡Comencemos!

Los diccionarios son otro tipo de estructura donde lo importante es al acceso a los elementos por su contenido. Nosotros agregamos un elemento a un diccionario para poder encontrarlo cuando lo necesitemos de forma eficiente. Un diccionario almacena pares de valores que constan de una llave y un valor (key-value) la llave es la que nos da acceso directo a el valor, de esta forma podemos almacenar datos para después encontrarlos fácilmente, de la forma en la que lo hicimos en el ejemplo del post anterior sobre saber si una palabra era una permutación de otra, nosotros usamos un diccionario para almacenar el conteo por cada letra. La letra era la llave (key) y la suma de la cantidad de esa letra era su valor (value).

Las operaciones principales en un diccionario son: search, insert, delete, para buscar, insertar y eliminar correspondientemente.

search(k) donde k es la llave que deseamos buscar, regresa el valor asociado a esa llave.

insert(k,x) donde k es la llave y x es el valor que deseamos insertar, agrega este par al diccionario.

delete(k,x) done k es la llave y x es el valor que deseamos borrar, remueve el par del diccionario.

Los diccionarios pueden ser implementados de distintas formas, se puede usar un array, una linked list, una combinación de ambas como en el ejemplo que planteamos sobre almacenar los usuarios de una aplicación, o con nuevas formas como lo son los hash-tables.

Una estructura hash table es un diccionario que implementa una función hash a la cuál le pasamos una cadena de caracteres (string) y esta nos devuelve un valor numérico asociado a esa cadena de caracteres.

Una función hash hace un mapeo de strings a números que debe ser consistente, lo que significa que cada string que entre a la función regresará siempre el mismo número. Además debe poder mapear distintas strings a distintos números por lo que, para una string dada en el mejor caso posible debe mapearse a un número distinto.

Función Hash
Retorna distintos números para las distintas strings"Marcela" -> 3
"Pedro"   -> 5
"Lola"    -> 0Siempre retorna 3 para el string "Marcela"
"Marcela" -> 3

Para un mejor entendimiento sobre qué es y cómo implementar una función hash les recomiendo leer: Capítulo 3 Data Structures – 3.7 Hashing and Strings, del libro The Algorithm Design Manual de Steven S. Skiena.

Un hash table se puede implementar con un array y una función hash, pero de esta forma nuestro hash table sería muy simple y pronto encontraríamos complicaciones. Nuestro array serviría para almacenar los valores que deseamos y la función hash debería retornar un número por cada string dada que se encuentre dentro del número de casillas en nuestro array.

En nuestro ejemplo anterior si nosotros tenemos un array de tamaño 10 y nosotros pasamos a la función hash “Marcela”, entonces el número 3 corresponde a la casilla número 3 del array, de mode que array[3] = valor a guardar. Si nosotros fuéramos a guardar el password de un usuario podríamos hacerlo en un hash table, el valor que se almacenará en el array será el password y sólo tenemos que encargarnos de que nuestra función hash sea lo suficientemente buena para retornar un número consistente y no repetido por cada string que le mandemos como llave (key), suena fácil, ¿no?.

Analicemos, ¿qué tan factible es lograr crear una función hash que nunca colisione con las disitintas strings pasadas como llaves y que retorne números dentro del alcance de nuestro array?, mucho dependerá de los datos que querramos mapear para almacenar, pero si quisiéramos un estructura genérica para cualquier tipo de dato esto sería difícil de conseguir por lo que podemos pensar en que en algún momento podemos tener una colisión y podemos entonces enfocarnos en manejar las colisiones.

Una forma fácil de manejar colisiones es a través del uso de linked lists, sí esas que ya vimos antes. Si en vez de almacenar el dato directamente en la casilla del array, almacenamos una linked list que almacenará todos los valores que caigan en esa casilla podemos entonces tener más de un valor por casilla, y así para cualquier colisión lo único que tendríamos que hacer es mapear a la casilla y a su llave para obtener ese valor. Esto no quita la importancia de mantener una función hash lo suficientemente buena para que en el mejor de los casos nunca colisione y así ayudar a la complejidad de la hash table al momento de obtener datos de ella.

Otro factor que debemos considerar es el el tamaño del array, ¿qué pasaría si intentamos insertar un nuevo par llave-valor y ya no queda espacio en el array?, en este caso debemos controlar el factor de carga o load factor, cada que insertemos un nuevo par debemos revisar el número de casillas restantes de nuestro array y de esa forma llegar a un valor que nos indique que es momento de crecer el array, de la misma forma en la que se haría con un dynamic array.

La forma de obtener el factor de carga de nuestro array es dividiendo el número de casillas ocupadas entre el número total de casillas, si el resultado es mayor o igual a 0.75 entonces debemos crecer el array. Este valor es un valor obtenido como “promedio” para este tipo de problemas así que podemos tomarlo como una buena práctica para nuestra implementación.

En la mayoría de problemas de almacenamiento de datos el uso de diccionarios reduce la complejidad de búsqueda de datos, es por eso que es una de las estructuras de datos más importantes en ciencias de la computación. Es comúnmente usada en cachés y bases de datos de alto performance y los hash tables no son la única forma de implementación, también se puede hacer mediante árboles y skip lists.

Ya he mencionado 5 estructuras de datos hasta ahora, he comentado sobre cuáles por sus características son mejores para búsquedas y actualización de datos, es por eso que ahora veremos una estructura que permita esta flexibilidad para buscar y actualizar datos de forma eficiente.

Comencemos por definir un tree (árbol). Un árbol es una estructura que consta de nodos y hojas. Cada nodo está conectado a otro nodo de forma jerárquica existiendo nodos “padre” y nodos “hijo” en distintos niveles, de modo que podamos crear una jerarquía desde un nodo raíz (root) hasta un último nivel de nodos hijo. Un tree, en realidad es un caso específico de un grafo, pero eso lo veremos más delante.

Ahora bien, un binary search tree (árbol de búsqueda binaria, BST), como su nombre lo dice, es un árbol que nos permitirá hacer búsquedas binarias, pero ¿a qué nos referimos con binarias? Bueno, pues el término binario se define como un compuesto de 2 partes, por lo tanto nuestro árbol estará seccionado en 2 partes, la parte de la izquierda y la parte de la derecha partiendo de un nodo raíz. En un árbol binario, a la izquierda se encuentran los nodos cuyo valor es menor al del nodo raíz, y a la derecha los de mayor valor, de forma que: un árbol binario sólo acepta tener como máximo 2 nodos hijo (izquierda y derecha). Y ¿por qué esta estructura sería flexible para buscar y para actualizar datos?, al tener sólo 2 partes en dónde buscar es más fácil encontrar un elemento.

Juguemos un poco a adivinar el número que estoy pensando entre 1 y 20, ¿cómo podrías adivinar?, pues claro, intentando un número en ese rango, si dices 3, y yo digo no, el número que estoy pensando es más grande, ¿qué otro número dirías?, un acercamiento sería continuar mencionando uno por uno hasta que lo atines: ¿es el 4? no, ¿es el 5? no, ¿es el 6? no, ¿es el 7? no, ¿es el 8? no, ¿es el 9? si, ¡ta tan! adivinaste después de 7 intentos, imagina que hubiera pensado el número 20, hubieran sido demasiados intentos, entonces, ¿podrías mejorar el número de intentos la próxima vez?, si, si hacemos una búsqueda binaria por menores y mayores. Así la próxima vez que pregunte qué numero estoy pensando entre 1 y 20 podrías comenzar por dividir a la mitad y preguntar, ¿es el 10? y yo diría no, es más chico, entonces sabes que debes buscar números entre 1 y 9 por lo que si divides en dos partes de nuevo el siguiente número sería el 5, ese tampoco es pero es mayor que 5, entonces el siguiente número entre 5 y 9 sería 7, que tampoco es pero es mayor, continua por la mitad y sería el 8 que no es pero es mayor así que la última opción que queda es 9. 

El número de intentos se redujo a 5, que aún son muchos pero si el número que hubiera pensando hubiera sido el 7 hubieras adivinado sólo en 3 intentos.

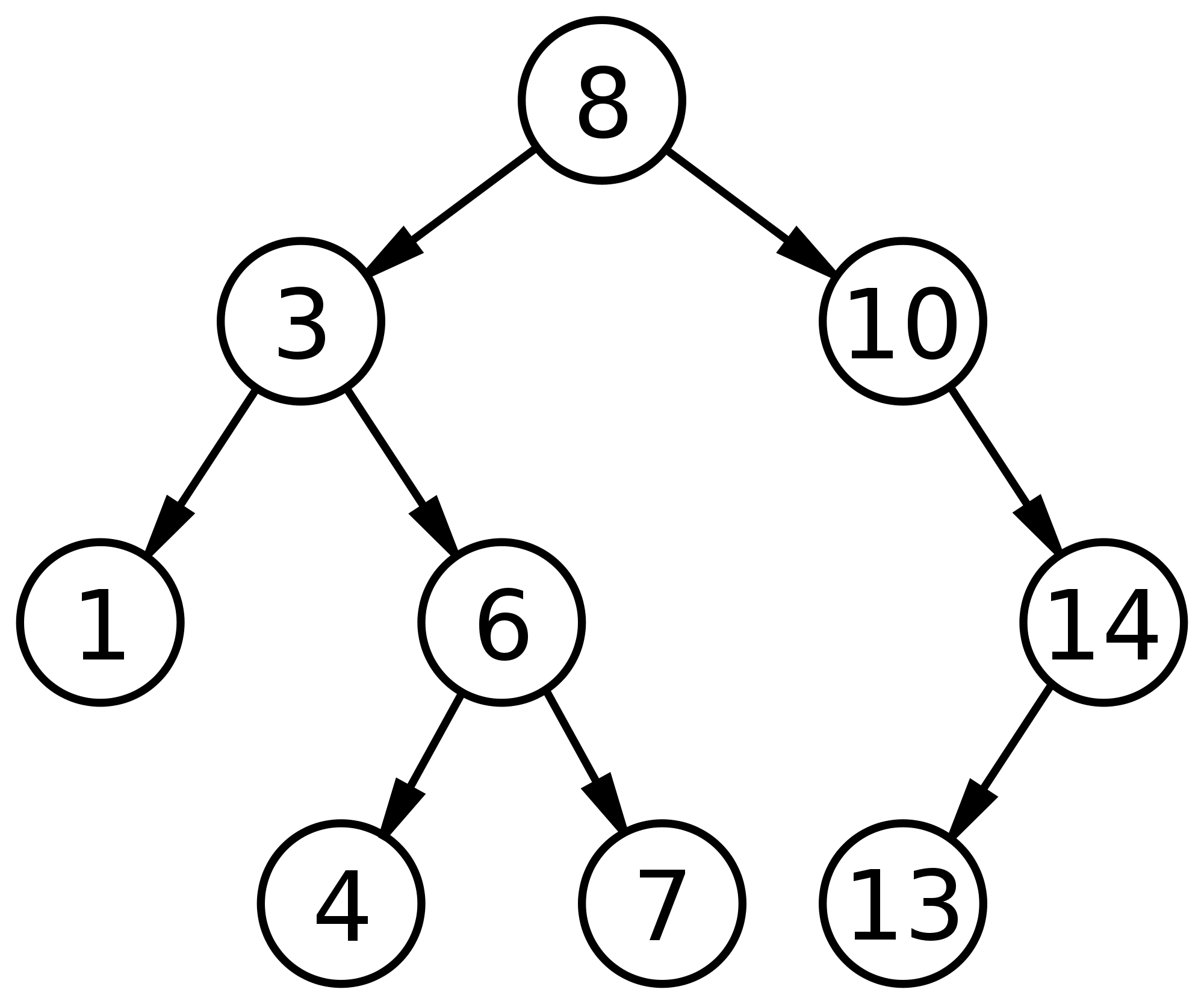
Ahora ya sabes cómo buscar de forma binaria un dato, pero esto realmente podrías hacerlo en un array que contenga los 20 números, dividiendo en mitad el array hasta encontrar el que buscas, ¡ah! pero estás olvidando la flexibilidad para actualizar un dato, en un array actualizar datos es muy costoso pues son estructuras de tamaño fijo y a pesar que el acceso es muy rápido insertar o eliminar “constantemente” no es eficiente, es por eso que los árboles funcionan como lo hacen las linked lists, manteniendo un apuntador (pointer) a sus nodos hijos y separando siempre entre mayores y menores por lo que la estructura base de un árbol sería un nodo raíz o padre y sus nodos hijos, el menor a la izquierda y el mayor a la derecha (como se ve en la imagen en el tercer nivel en el nodo 6 con sus hijos 4 y 7 correspondientemente). Al mantener punteros hacia los nodos hijos es muy fácil insertar uno nuevo, por ejemplo, si deseamos agregar el número 5 en ese árbol de la imagen, ¿en dónde se intertaría?. 

El número 5 es menor que el nodo raíz 8, por lo tanto debe ir a la izquierda del árbol, pero 5 > 3 a la derecha, 5 < 6 a la izquierda y 5 > 4, así que el 5 se insertaría como un nuevo nodo hijo del nodo 4 a su derecha. Y si quisiéramos remover el nodo 6, ¿cómo lo haríamos?, lo primero es buscar el 6 que es menor que 8 entonces vamos a la izquierda, pero 6 > 3 entonces a la derecha y una vez encontrado, como este nodo tiene hijos debemos elegir un nuevo “padre” para esos hijos, en este punto existen varias técnicas que definen las reglas para elegir al nuevo padre, yo elegiré tomar el nodo hijo que no tenga nodos hijos, que en este caso sería el 7, ahora el nodo 3 apunta a la derecha a 7 y 7 tiene a su izquierda al nodo 4, sin romper el esquema de mayores y menores hemos removido el nodo 6 sin mayor problema.

En la imagen de la izquierda podemos observar de qué forma podemos representar un árbol con apuntadores de la misma forma en la que lo haría una linked list, pero en vez de mantener secuencias de datos mantenemos una jerarquía. Las operaciones fundamentales sobre un BST son: insert(x), remove(x), y search(x) como ya hemos visto en los ejemplos anteriores sobre insertar, remover y buscar en un árbol binario. Al igual que las linked lists, los árboles requieren de más espacio en memoria si mantenemos tantos punteros, esto es algo a considerar si decidimos usarla.

Los árboles de búsqueda binaria o BST, son muy comúnes debido a su fácil representación binaria para hacer búsquedas y actualización de datos de forma eficiente, ayudan a mantener una gran cantidad de datos de forma ordenada y aseguran una complejidad algorítimica muy baja en estos casos, sin embargo no debemos olvidar otros conceptos de árboles como el balance. Cuando hablo de balance me refiero a que para que un BST sea “eficiente” debe estar balanceado, o que debe mantener (por lo menos) el mismo número de niveles de nodos en ambas partes. Imagina qué pasaría si en el ejemplo de adivinar el número insertamos del 1 al 20 consecutivamente en un árbol, ¿el árbol estaría balanceado? la respuesta es no, porque si comenzamos insertando el 1 como nodo raíz y continuamos con el 2 este se insertaría a su derecha y el 3 a la derecha del 2 y el 4 a la derecha del 3 y así sucesivamente hasta tener una secuencia 1=>2=>3=>4=>5 … 19=>20, esto realmente no representa un árbol binario balanceado, si qusiéramos buscar un número tendríamos que recorrer todos los niveles hasta encontrar el número lo cuál no es nada eficiente.

 La forma correcta de balancear este árbol es hacerlo de la misma forma en la que buscamos, ¿cuál es la mitad de 20? es 10, entonces hacemos al 10 el nodo raíz y dividimos en 2 partes la inserción, de modo que 10 tiene como hijos a 5<=10=>15, 5 tiene como hijos a 2<=5=>7, 15 tiene como hijos a 12<=15=>17 … y así hasta balancear el árbol por completo. Ahora sí, si buscamos un número en este árbol balanceado lo podremos hacer de forma eficiente sin tener que recorrer todos los niveles en el peor de los casos.

Los árboles son estructuras poderosas y los BST son los más usados, sin embargo no es la única forma de representar datos sobre un árbol. Puesto que podemos definir jerarquías con distintas reglas, para una representación específica un nodo padre puede llegar a tener 6 hijos o más y así llegar a tener diferentes tipos de árboles como son los Tries, o la representación del código morse en un árbol que nos permita traducir mensajes en morse al idioma deseado, ambas representaciones de datos en árboles nos permiten la búsqueda fácil y rápida de elementos.

Ya había mencionado que un árbol es una representación específica de un grafo, entonces ¿qué es un grafo?.

En palabras de Steven S. Skiena:

Más precisamente:

Un grafo G = (V, E) consiste en un conjunto de vértices (vertex/vertices) V junto con un conjunto E de pares de vértices o bordes (edges).

Los grafos son importantes porque se pueden usar para representar esencialmente cualquier relación, por ejemplo: las calles en una ciudad, las computadoras conectadas en un red local, las conexiones de vuelos nacionales o internacionales de un aeropuerto a otros, un circuito eléctrico, etc.

En un grafo podemos representar la conexión de muchos nodos, los vértices o vertex y bordes o edges son el conjunto de elementos dentro de un grafo y no existe una representación única, por el contrario existen muchas clasificaciones, tan grande es el estudio de estas representaciones que existe toda un teoría de grafos para definirlos, es por eso que me limitaré a mencionar sólo lo más importante y lo que debes saber para identificar problemas que se resuelvan con grafos.

Skiena claramente menciona que se puede representar casi cualquier relación con el uso de grafos, lo podemos comprobar de muchas formas piensa en todo lo que puedes relacionar, lo primero que te venga a la mente, ¿qué tal tu árbol genealógico?, los vertices son cada uno de tus familiares y los edges la realación que existe entre cada familiar (padre, hijo, abuelo, primo, etc), y ¿qué tal las cafeterías más cercanas a tu casa?, cada vertex es una cafetería y los edges es el tiempo que tardas en llegar a ellas, o también puede ser la distancia, y así muchos otros casos tan comunes en el día a día.

Ahora, ¿por qué querríamos usar un grafo como estructura de datos? 

Como ya te habrás dado cuenta las “relaciones” entre datos existen en casi todos los tipos de datos que podemos llegar a querer organizar y más si en ciencias de la computación siempre tratamos de modelar los elementos que existen a nuestro alrededor y cómo nos relacionamos con ellos, desde un mapa geográfico, relaciones humanas, productos en un inventario, formas de pago, idiomas, y problemas en ciencias exactas como la física y matemáticas, un sin fin de posibilidades. Si casi todo lo podemos abstraer en grafos entonces ésta estructura es verdaderamente importante y útil.

Los grafos se pueden representar de dos formas principalmente: una lista o una matriz de adyacencia (adjacency list or matrix). Ambas formas son muy eficientes en casos específicos, en un matriz podemos rápidamente agregar nuevos edges entre vertices, y saber si un vertex está conectado a otro sería instantáneo por el rápido acceso aleatorio que ofrece una matriz, y ya que:

Podemos representar G usando una matriz n × n M, donde el elemento M [i, j] = 1 si (i, j) es un edge de G, y 0 si no lo es.

pero imaginen ahora un grafo con 2,000 vertices, representar un matriz de n x n sería en verdad costoso en recursos de memoria, aunque podría funcionar si la lectura y escritura son a disco con el costo que esto conlleve.

Por otro lado las listas de adyacencia mantienen punteros los cuáles sabemos que también requieren memoria, pero al ser elementos que no son contiguamente asignados y están dispersos en memoria la eficiencia de recursos mejora ya que sólo es necesario mantener la cantidad de vertices y los edges que existan entre ellos. Sin embargo, en las listas de adyacencia es más difícil saber si un vertex está conectado a otro ya que requerimos buscar en la lista el vertex deseado y si existe una conexión, pero es más fácil modelar un grafo de esta forma. Si usamos un diccionario para representar un grafo donde la key es el vertex y el value es una linked list de todos sus edges (que es lo más común para representar una lista de adayacencia) la eficiencia de búsqueda de los vertices y sus edges sería relativamente rápida.

En términos generales para problemas no tan específicos las listas de adyacencia son mejores.

Retomando el punto de “saber si un vertex está conectado a otro”, que es una operación muy frecuente dentro de los grafos, expondré el siguiente ejemplo (el más común que pueden encontrar): imaginen que Facebook representa a sus amigos en un grafo, los vertices son tú y tus amigos y los edges su relación de amistad, así si yo “Marcela” soy amiga de “Pedro” y de “Mariana”, tenemos una relación no direccionada (undirected) puesto que Yo soy amiga de Pedro y Pedro me tiene como amiga, pero esto no podría ser en una relación en mi árbol genealógico ya que yo sólo puedo ser hija de mi padre pero no al revés, en este caso la relación es direccionada (directed), de “mi a mi padre” es un relación de padre, y de “mi padre a mi” es una relación de hijo la relación lleva una dirección o sentido asignado. Bien ahora imaginemos que queremos saber si existe alguna conexión de amigos entre “Juan” y yo. “Pedro” tiene a “Gaby” y “Pablo” de amigos y “Gaby” tiene a “Juan” de amigo.

Lista de adyacencia

Marcela => Pedro, Mariana

Pedro => Gaby, Pablo
Gaby => Juan

En una lista de adyacencia podemos saber las conexiones yendo a través de los vertices, comenzamos con mis edges Pedro y Mariana, si vamos con Pedro entonces tenemos que revisar a Gaby y Pablo, si vamos con Gaby, entonces llegaremos a Juan, eso significa que si existe un “camino” de relación de amistad entre Juan y Yo, y si quisiéramos saber si Juan y Yo somo amigos directamente, sólo basta con revisar mis edges, no lo encontraríamos pues yo sólo soy amiga de Pedro y Mariana.

Como este tipo de problemas existen tantos que se pueden abordar con grafos, como el ejemplo de las cafeterías cerca de mi casa, ¿qué pasa si quiero saber cuál es la más cercana en tiempo o distancia? en este caso los edges tienen asignados un “peso” que sería el tiempo o la distancia, si quiero saber cuál es la más cercana entonces debo tomar en cuenta esos pesos y obtener el menor de ellos, a este tipo de relaciones entre vertices se les llama con peso (weighted) o sin peso (unweighted), el grafo de mis amistades no tiene pesos asignados pero el de las cafeterías si lo tien, y para ese tipo de grafos existen cierto tipo de “algoritmos” que se pueden aplicar para resolver cuál es el menor o mayor de los casos, pero esa es hariana de otro costal, por ahora basta con que sepas cómo representar datos en grafos, qué estructuras de datos usar para su implementación y qué tipo de problemas puedes resolver con ellos.

Diccionarios, árboles y grafos, tres estructuras sumamente poderosas y que a su vez añaden un nivel de complejidad más, construidas en base a otras estructuras como arrays y linked lists tomando lo mejor de cada una y permitiéndonos mejorar las operaciones de búsqueda, inserción y remoción de elementos así como la organización y relaciones entre datos.

Sin duda, tener en cuenta lo que podemos hacer y representar con cada estructura además de lo que nos ayudan a mejorar (para qué sirven) nos hará mejores programadores.